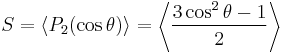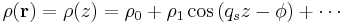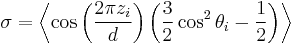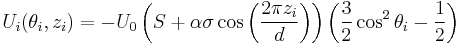Liquid crystal

Schlieren texture of liquid crystal nematic phase
Schlieren texture on an LCD screen of a PlayStation Portable viewed through a circular polarizer

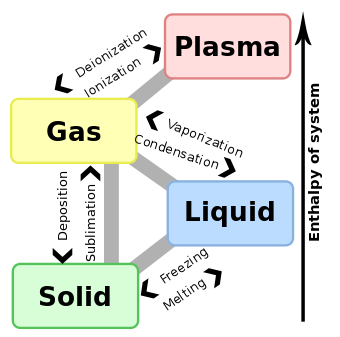
Liquid crystals (LCs) are a state of matter that have properties between those of a conventional liquid and those of a solid crystal.[1] For instance, an LC may flow like a liquid, but its molecules may be oriented in a crystal-like way. There are many different types of LC phase, which can be distinguished by their different optical properties (such as birefringence). When viewed under a microscope using a polarized light source, different liquid crystal phases will appear to have distinct textures. The contrasting areas in the textures correspond to domains where the LC molecules are oriented in different directions. Within a domain, however, the molecules are well ordered. LC materials may not always be in an LC phase (just as water may turn into ice or steam).

Liquid crystals can be divided into thermotropic, lyotropic and metallotropic phases. Thermotropic and lyotropic LCs consist of organic molecules. Thermotropic LCs exhibit a phase transition into the LC phase as temperature is changed. Lyotropic LCs exhibit phase transitions as a function of both temperature and concentration of the LC molecules in a solvent (typically water). Metallotropic LCs are composed of both organic and inorganic molecules; their LC transition depends not only on temperature and concentration, but also on the inorganic-organic composition ratio.

Examples of liquid crystals can be found both in the natural world and in technological applications. Most modern electronic displays are liquid crystal based. Lyotropic liquid-crystalline phases are abundant in living systems. For example, many proteins and cell membranes are LCs. Other well-known LC examples are solutions of soap and various related detergents, as well as tobacco mosaic virus.

Contents

History

In 1888, Austrian botanical physiologist Friedrich Reinitzer, working at the Charles University in Prague, examined the physico-chemical properties of various derivatives of cholesterol, which are now known as cholesteric liquid crystals. Previously, other researchers had observed distinct color effects when cooling cholesterol derivatives just above the freezing point, but had not associated it with a new phenomenon. Reinitzer perceived that color changes in a derivative cholesteryl benzoate were not the most peculiar feature. He found that cholesteryl benzoate does not melt in the same manner as other compounds, but has two melting points. At 145.5 °C (293.9 °F) it melts into a cloudy liquid, and at 178.5 °C (353.3 °F) it melts again and the cloudy liquid becomes clear. The phenomenon is reversible. Seeking help from a physicist, on March 14, 1888, he wrote to Otto Lehmann, at that time a Privatdozent in Aachen. They exchanged letters and samples. Lehmann examined the intermediate cloudy fluid, and reported seeing crystallites. Reinitzer's Viennese colleague von Zepharovich also indicated that the intermediate "fluid" was crystalline. The exchange of letters with Lehmann ended on April 24, with many questions unanswered. Reinitzer presented his results, with credits to Lehmann and von Zepharovich, at a meeting of the Vienna Chemical Society on May 3, 1888.[2]

By that time, Reinitzer had discovered and described three important features of cholesteric liquid crystals (the name coined by Georges Friedel in 1922): the existence of two melting points, the reflection of circularly polarized light, and the ability to rotate the polarization direction of light.

After his accidental discovery, Reinitzer did not pursue studying liquid crystals further. The research was continued by Lehmann, who realized that he had encountered a new phenomenon and was in a position to investigate it: In his postdoctoral years he had acquired expertise in crystallography and microscopy. Lehmann started a systematic study, first of cholesteryl benzoate, and then of related compounds which exhibited the double-melting phenomenon. He was able to make observations in polarized light, and his microscope was equipped with a hot stage (sample holder equipped with a heater) enabling high temperature observations. The intermediate cloudy phase clearly sustained flow, but other features, particularly the signature under a microscope, convinced Lehmann that he was dealing with a solid. By the end of August 1889 he had published his results in the Zeitschrift für Physikalische Chemie.[3]

Lehmann's work was continued and significantly expanded by the German chemist Daniel Vorländer, who from the beginning of 20th century until his retirement in 1935, had synthesized most of the liquid crystals known. However, liquid crystals were not popular among scientists and the material remained a pure scientific curiosity for about 80 years.[4]

Chemical structure of N-(4-Methoxybenzylidene)-4-butylaniline (MBBA) molecule

In 1969, Hans Kelker succeeded in synthesizing a substance that had a nematic phase at room temperature, MBBA, which is one of the most popular subjects of liquid crystal research.[5] The next step to commercialization of liquid crystal displays was the synthesis of further chemically stable substances (cyanobiphenyls) with low melting temperatures by George Gray.[6]

In 1991, when liquid crystal displays were already well established, Pierre-Gilles de Gennes received the Nobel Prize in physics "for discovering that methods developed for studying order phenomena in simple systems can be generalized to more complex forms of matter, in particular to liquid crystals and polymers".[7]

Liquid crystal phases

The various LC phases (called mesophases) can be characterized by the type of ordering. One can distinguish positional order (whether molecules are arranged in any sort of ordered lattice) and orientational order (whether molecules are mostly pointing in the same direction), and moreover order can be either short-range (only between molecules close to each other) or long-range (extending to larger, sometimes macroscopic, dimensions). Most thermotropic LCs will have an isotropic phase at high temperature. That is that heating will eventually drive them into a conventional liquid phase characterized by random and isotropic molecular ordering (little to no long-range order), and fluid-like flow behavior. Under other conditions (for instance, lower temperature), an LC might inhabit one or more phases with significant anisotropic orientational structure and short-range orientational order while still having an ability to flow.[8][9]

The ordering of liquid crystalline phases is extensive on the molecular scale. This order extends up to the entire domain size, which may be on the order of micrometers, but usually does not extend to the macroscopic scale as often occurs in classical crystalline solids. However some techniques, such as the use of boundaries or an applied electric field, can be used to enforce a single ordered domain in a macroscopic liquid crystal sample. The ordering in a liquid crystal might extend along only one dimension, with the material being essentially disordered in the other two directions.[10][11]

Thermotropic liquid crystals

Thermotropic phases are those that occur in a certain temperature range. If the temperature rise is too high, thermal motion will destroy the delicate cooperative ordering of the LC phase, pushing the material into a conventional isotropic liquid phase. At too low temperature, most LC materials will form a conventional crystal.[8][9] Many thermotropic LCs exhibit a variety of phases as temperature is changed. For instance, a particular type of LC molecule (called mesogen) may exhibit various smectic and nematic (and finally isotropic) phases as temperature is increased. An example of a compound displaying thermotropic LC behavior is para-azoxyanisole.[12]

Nematic phase

Alignment in a nematic phase.
Phase transition between a nematic (left) and smectic A (right) phases observed between crossed polarizers. The black color corresponds to isotropic medium.

One of the most common LC phases is the nematic. The word nematic comes from the Greek νημα (nema), which means "thread". This term originates from the thread-like topological defects observed in nematics, which are formally called 'disclinations'. Nematics also exhibit so-called hedgehog topological defects. In a nematic phase, the calamitic or rod-shaped organic molecules have no positional order, but they self-align to have long-range directional order with their long axes roughly parallel.[13] Thus, the molecules are free to flow and their center of mass positions are randomly distributed as in a liquid, but still maintain their long-range directional order. Most nematics are uniaxial: they have one axis that is longer and preferred, with the other two being equivalent (can be approximated as cylinders or rods). However, some liquid crystals are biaxial nematics, meaning that in addition to orienting their long axis, they also orient along a secondary axis.[14] Nematics have fluidity similar to that of ordinary (isotropic) liquids but they can be easily aligned by an external magnetic or electric field. Aligned nematics have the optical properties of uniaxial crystals and this makes them extremely useful in liquid crystal displays (LCD).[15]

Smectic phases

Schematic of alignment in the smectic phases. The smectic A phase (left) has molecules organized into layers. In the smectic C phase (right), the molecules are tilted inside the layers.

The smectic phases, which are found at lower temperatures than the nematic, form well-defined layers that can slide over one another in a manner similar to that of soap. The smectics are thus positionally ordered along one direction. In the Smectic A phase, the molecules are oriented along the layer normal, while in the Smectic C phase they are tilted away from the layer normal. These phases are liquid-like within the layers. There are many different smectic phases, all characterized by different types and degrees of positional and orientational order.[8][9]

Chiral phases

Schematic of ordering in chiral liquid crystal phases. The chiral nematic phase (left), also called the cholesteric phase, and the smectic C* phase (right).

The chiral nematic phase exhibits chirality (handedness). This phase is often called the cholesteric phase because it was first observed for cholesterol derivatives. Only chiral molecules (i.e., those that lack inversion symmetry) can give rise to such a phase. This phase exhibits a twisting of the molecules perpendicular to the director, with the molecular axis parallel to the director. The finite twist angle between adjacent molecules is due to their asymmetric packing, which results in longer-range chiral order. In the smectic C*phase (an asterisk denotes a chiral phase), the molecules have positional ordering in a layered structure (as in the other smectic phases), with the molecules tilted by a finite angle with respect to the layer normal. The chirality induces a finite azimuthal twist from one layer to the next, producing a spiral twisting of the molecular axis along the layer normal.[8][10][11]

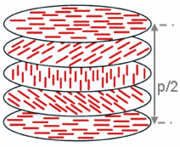
Chiral nematic phase; p refers to the chiral pitch (see text)

The chiral pitch, p, refers to the distance over which the LC molecules undergo a full 360° twist (but note that the structure of the chiral nematic phase repeats itself every half-pitch, since in this phase directors at 0° and ±180° are equivalent). The pitch, p, typically changes when the temperature is altered or when other molecules are added to the LC host (an achiral LC host material will form a chiral phase if doped with a chiral material), allowing the pitch of a given material to be tuned accordingly. In some liquid crystal systems, the pitch is of the same order as the wavelength of visible light. This causes these systems to exhibit unique optical properties, such as Bragg reflection and low-threshold laser emission,[16] and these properties are exploited in a number of optical applications.[10][17] For the case of Bragg reflection only the lowest-order reflection is allowed if the light is incident along the helical axis, whereas for oblique incidence higher-order reflections become permitted. Cholesteric liquid crystals also exhibit the unique property that they reflect circularly polarized light when it is incident along the helical axis and elliptically polarized if it comes in obliquely.[18]

Blue phases

Blue phases are special types of liquid crystal phases that appear in the temperature range between a chiral nematic phase and an isotropic liquid phase. Blue phases have a regular three-dimensional cubic structure of defects with lattice periods of several hundred nanometers, and thus they exhibit selective Bragg reflections in the wavelength range of light (visible part of electromagnetic radiation) corresponding to the cubic lattice. Although blue phases are of interest for fast light modulators or tunable photonic crystals, the very narrow temperature range within which blue phases exist, usually less than a few kelvin, has always been a problem. Recently the stabilization of blue phases over a temperature range of more than 60 K including room temperature (260–326 K) could be demonstrated.[19][20]

Furthermore, electro-optical switching with response times of the order of 10−4 s for the stabilized blue phases at room temperature has been shown.[21]

In May 2008, it was announced that the first Blue Phase Mode LCD panel had been developed.[22]

Discotic phases

Disk-shaped LC molecules can orient themselves in a layer-like fashion known as the discotic nematic phase. If the disks pack into stacks, the phase is called a discotic columnar. The columns themselves may be organized into rectangular or hexagonal arrays. Chiral discotic phases, similar to the chiral nematic phase, are also known.

Lyotropic liquid crystals

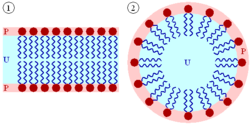
Structure of lyotropic liquid crystal. The red heads of surfactant molecules are in contact with water, whereas the tails are immersed in oil (blue): bilayer (left) and micelle (right)

A lyotropic liquid crystal consists of two or more components that exhibit liquid-crystalline properties in certain concentration ranges. In the lyotropic phases, solvent molecules fill the space around the compounds to provide fluidity to the system. In contrast to thermotropic liquid crystals, these lyotropics have another degree of freedom of concentration that enables them to induce a variety of different phases.

A compound, which has two immiscible hydrophilic and hydrophobic parts within the same molecule, is called an amphiphilic molecule. Many amphiphilic molecules show lyotropic liquid-crystalline phase sequences depending on the volume balances between the hydrophilic part and hydrophobic part. These structures are formed through the micro-phase segregation of two incompatible components on a nanometer scale. Soap is an everyday example of a lyotropic liquid crystal.

The content of water or other solvent molecules changes the self-assembled structures. At very low amphiphile concentration, the molecules will be dispersed randomly without any ordering. At slightly higher (but still low) concentration, amphiphilic molecules will spontaneously assemble into micelles or vesicles. This is done so as to 'hide' the hydrophobic tail of the amphiphile inside the micelle core, exposing a hydrophilic (water-soluble) surface to aqueous solution. These spherical objects do not order themselves in solution, however. At higher concentration, the assemblies will become ordered. A typical phase is a hexagonal columnar phase, where the amphiphiles form long cylinders (again with a hydrophilic surface) that arrange themselves into a roughly hexagonal lattice. This is called the middle soap phase. At still higher concentration, a lamellar phase (neat soap phase) may form, wherein extended sheets of amphiphiles are separated by thin layers of water. For some systems, a cubic (also called viscous isotropic) phase may exist between the hexagonal and lamellar phases, wherein spheres are formed that create a dense cubic lattice. These spheres may also be connected to one another, forming a bicontinuous cubic phase.

The objects created by amphiphiles are usually spherical (as in the case of micelles), but may also be disc-like (bicelles), rod-like, or biaxial (all three micelle axes are distinct). These anisotropic self-assembled nano-structures can then order themselves in much the same way as liquid crystals do, forming large-scale versions of all the thermotropic phases (such as a nematic phase of rod-shaped micelles).

For some systems, at high concentrations, inverse phases are observed. That is, one may generate an inverse hexagonal columnar phase (columns of water encapsulated by amphiphiles) or an inverse micellar phase (a bulk liquid crystal sample with spherical water cavities).

A generic progression of phases, going from low to high amphiphile concentration, is:

Even within the same phases, their self-assembled structures are tunable by the concentration: for example, in lamellar phases, the layer distances increase with the solvent volume. Since lyotropic liquid crystals rely on a subtle balance of intermolecular interactions, it is more difficult to analyze their structures and properties than those of thermotropic liquid crystals.

Similar phases and characteristics can be observed in immiscible diblock copolymers.

Metallotropic liquid crystals

Liquid crystal phases can also be based on low-melting inorganic phases like ZnCl2 that have a structure formed of linked tetrahedra and easily form glasses. The addition of long chain soap-like molecules leads to a series of new phases that show a variety of liquid crystalline behavior both as a function of the inorganic-organic composition ratio and of temperature. This class of materials has been named metallotropic.[23]

Biological liquid crystals

Lyotropic liquid-crystalline phases are abundant in living systems, the study of which is referred to as polymorphism. Accordingly, lyotropic liquid crystals attract particular attention in the field of biomimetic chemistry. In particular, biological membranes and cell membranes are a form of liquid crystal. Their constituent molecules (e.g., phospholipids) are perpendicular to the membrane surface, yet the membrane is flexible. These lipids vary in shape (see page on lipid polymorphism). The constituent molecules can inter-mingle easily, but tend not to leave the membrane due to the high energy requirement of this process. Lipid molecules can flip from one side of the membrane to the other, this process being catalyzed by flippases and floppases (depending on the direction of movement). These liquid crystal membrane phases can also host important proteins such as receptors freely "floating" inside, or partly outside, the membrane, e.g. CCT.

Many other biological structures exhibit LC behavior. For instance, the concentrated protein solution that is extruded by a spider to generate silk is, in fact, a liquid crystal phase. The precise ordering of molecules in silk is critical to its renowned strength. DNA and many polypeptides can also form LC phases and this too forms an important part of current academic research.

Pattern formation in liquid crystals

Anisotropy of liquid crystals is a property not observed in other fluids. This anisotropy makes flows of liquid crystals behave more differentially than those of ordinary fluids. For example, injection of a flux of a liquid crystal between two close parallel plates (viscous fingering), causes orientation of the molecules to couple with the flow, with the resulting emergence of dendritic patterns.[24] This anisotropy is also manifested in the interfacial energy (surface tension) between different liquid crystal phases. This anisotropy determines the equilibrium shape at the coexistence temperature, and is so strong that usually facets appear. When temperature is changed one of the phases grows, forming different morphologies depending on the temperature change.[25] Since growth is controlled by heat diffusion, anisotropy in thermal conductivity favors growth in specific directions, which has also an effect on the final shape.[26]

Theoretical treatment of liquid crystals

Microscopic theoretical treatment of fluid phases can become quite complicated, owing to the high material density, meaning that strong interactions, hard-core repulsions, and many-body correlations cannot be ignored. In the case of liquid crystals, anisotropy in all of these interactions further complicates analysis. There are a number of fairly simple theories, however, that can at least predict the general behavior of the phase transitions in liquid crystal systems.

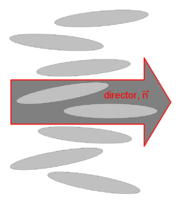
Director

As we already saw above, the nematic liquid crystals are composed of rod-like molecules with the long axes of neighboring molecules aligned approximately to one another. To allow this anisotropic structure, a dimensionless unit vector n called the director, is introduced to represent the direction of preferred orientation of molecules in the neighborhood of any point. Because there is no physical polarity along the director axis, n and -n are fully equivalent.[8]

Order parameter

The local nematic director, which is also the local optical axis, is given by the spatial and temporal average of the long molecular axes

The description of liquid crystals involves an analysis of order. A tensor order parameter is used to describe the orientational order of a liquid crystal, although a scalar order parameter is usually sufficient to describe nematic liquid crystals. To make this quantitative, an orientational order parameter is usually defined based on the average of the second Legendre polynomial:

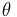S = \langle P_2(\cos \theta) \rangle = \left \langle \frac{3 \cos^2 \theta-1}{2} \right \rangle

where \theta is the angle between the LC molecular axis and the local director (which is the 'preferred direction' in a volume element of a liquid crystal sample, also representing its local optical axis). The brackets denote both a temporal and spatial average. This definition is convenient, since for a completely random and isotropic sample, S=0, whereas for a perfectly aligned sample S=1. For a typical liquid crystal sample, S is on the order of 0.3 to 0.8, and generally decreases as the temperature is raised. In particular, a sharp drop of the order parameter to 0 is observed when the system undergoes a phase transition from an LC phase into the isotropic phase.[27] The order parameter can be measured experimentally in a number of ways. For instance, diamagnetism, birefringence, Raman scattering, NMR and EPR can also be used to determine S.[11]

The order of a liquid crystal could also be characterized by using other even Legendre polynomials (all the odd polynomials average to zero since the director can point in either of two antiparallel directions). These higher-order averages are more difficult to measure, but can yield additional information about molecular ordering.[9]

A positional order parameter is also used to describe the ordering of a liquid crystal. It is characterized by the variation of the density of the center of mass of the liquid crystal molecules along a given vector. In the case of positional variation along the z-axis the density 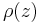\rho (z) is often given by:

\rho (\mathbf{r})=\rho (z)=\rho_0+\rho_1\cos\left (q_sz-\phi\right )+\cdots

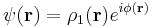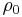The complex positional order parameter is defined as \psi (\mathbf{r})=\rho_1 (\mathbf{r})e^{i\phi(\mathbf{r})} and \rho_0 the average density. Typically only the first two terms are kept and higher order terms are ignored since most phases can be described adequately using sinusoidal functions. For a perfect nematic 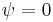\psi=0 and for a smectic phase \psi will take on complex values. The complex nature of this order parameter allows for many parallels between nematic to smectic phase transitions and conductor to superconductor transitions.[8]

Onsager hard-rod model

A simple model which predicts lyotropic phase transitions is the hard-rod model proposed by Lars Onsager. This theory considers the volume excluded from the center-of-mass of one idealized cylinder as it approaches another. Specifically, if the cylinders are oriented parallel to one another, there is very little volume that is excluded from the center-of-mass of the approaching cylinder (it can come quite close to the other cylinder). If, however, the cylinders are at some angle to one another, then there is a large volume surrounding the cylinder which the approaching cylinder's center-of-mass cannot enter (due to the hard-rod repulsion between the two idealized objects). Thus, this angular arrangement sees a decrease in the net positional entropy of the approaching cylinder (there are fewer states available to it).[28][29]

The fundamental insight here is that, whilst parallel arrangements of anisotropic objects lead to a decrease in orientational entropy, there is an increase in positional entropy. Thus in some case greater positional order will be entropically favorable. This theory thus predicts that a solution of rod-shaped objects will undergo a phase transition, at sufficient concentration, into a nematic phase. Although this model is conceptually helpful, its mathematical formulation makes several assumptions that limit its applicability to real systems.[29]

Maier-Saupe mean field theory

This statistical theory, proposed by Alfred Saupe and Wilhelm Maier, includes contributions from an attractive intermolecular potential from an induced dipole moment between adjacent liquid crystal molecules. The anisotropic attraction stabilizes parallel alignment of neighboring molecules, and the theory then considers a mean-field average of the interaction. Solved self-consistently, this theory predicts thermotropic nematic-isotropic phase transitions, consistent with experiment.[30][31][32]

McMillan's model

McMillan's model, proposed by William McMillan,[33] is an extension of the Maier-Saupe mean field theory used to describe the phase transition of a liquid crystal from a nematic to a smectic A phase. It predicts that the phase transition can be either continuous or discontinuous depending on the strength of the short-range interaction between the molecules. As a result, it allows for a triple critical point where the nematic, isotropic, and smectic A phase meet. Although it predicts the existence of a triple critical point, it does not successfully predict its value. The model utilizes two order parameters that describe the orientational and positional order of the liquid crystal. The first is simply the average of the second Legendre polynomial and the second order parameter is given by:

\sigma=\left\langle\cos\left (\frac{2\pi z_i}{d}\right )\left (\frac{3}{2}\cos^2\theta_i-\frac{1}{2}\right )\right\rangle

The values zi, θi, and d are the position of the molecule, the angle between the molecular axis and director, and the layer spacing. The postulated potential energy of a single molecule is given by:

U_i(\theta_i,z_i)=-U_0\left (S+\alpha\sigma\cos\left (\frac{2\pi z_i}{d}\right )\right )\left (\frac{3}{2}\cos^2\theta_i-\frac{1}{2}\right )

Here constant α quantifies the strength of the interaction between adjacent molecules. The potential is then used to derive the thermodynamic properties of the system assuming thermal equilibrium. It results in two self-consistency equations that must be solved numerically, the solutions of which are the three stable phases of the liquid crystal.[11]

Elastic continuum theory

In this formalism, a liquid crystal material is treated as a continuum; molecular details are entirely ignored. Rather, this theory considers perturbations to a presumed oriented sample. The distortions of the liquid crystal are commonly described by the Frank free energy density. One can identify three types of distortions that could occur in an oriented sample: (1) twists of the material, where neighboring molecules are forced to be angled with respect to one another, rather than aligned; (2) splay of the material, where bending occurs perpendicular to the director; and (3) bend of the material, where the distortion is parallel to the director and molecular axis. All three of these types of distortions incur an energy penalty. They are distortions that are induced by the boundary conditions at domain walls or the enclosing container. The response of the material can then be decomposed into terms based on the elastic constants corresponding to the three types of distortions. Elastic continuum theory is a particularly powerful tool for modeling liquid crystal devices.[34]

Effect of chirality

As already described, chiral LC molecules usually give rise to chiral mesophases. This means that the molecule must possess some form of asymmetry, usually a stereogenic center. An additional requirement is that the system not be racemic: a mixture of right- and left-handed molecules will cancel the chiral effect. Due to the cooperative nature of liquid crystal ordering, however, a small amount of chiral dopant in an otherwise achiral mesophase is often enough to select out one domain handedness, making the system overall chiral.

Chiral phases usually have a helical twisting of the molecules. If the pitch of this twist is on the order of the wavelength of visible light, then interesting optical interference effects can be observed. The chiral twisting that occurs in chiral LC phases also makes the system respond differently from right- and left-handed circularly polarized light. These materials can thus be used as polarization filters.[35]

It is possible for chiral LC molecules to produce essentially achiral mesophases. For instance, in certain ranges of concentration and molecular weight, DNA will form an achiral line hexatic phase. An interesting recent observation is of the formation of chiral mesophases from achiral LC molecules. Specifically, bent-core molecules (sometimes called banana liquid crystals) have been shown to form liquid crystal phases that are chiral.[36] In any particular sample, various domains will have opposite handedness, but within any given domain, strong chiral ordering will be present. The appearance mechanism of this macroscopic chirality is not yet entirely clear. It appears that the molecules stack in layers and orient themselves in a tilted fashion inside the layers. These liquid crystals phases may be ferroelectric or anti-ferroelectric, both of which are of interest for applications.[37][38]

Chirality can also be incorporated into a phase by adding a chiral dopant, which may not form LCs itself. Twisted-nematic or super-twisted nematic mixtures often contain a small amount of such dopants.

Applications of liquid crystals

See also: Liquid crystal display
Structure of liquid crystal display: 1 – vertical polarization filter, 2,4 – glass with electrodes, 3 – liquid crystals, 5 – horizontal polarization filter, 6 – reflector

Liquid crystals find wide use in liquid crystal displays, which rely on the optical properties of certain liquid crystalline substances in the presence or absence of an electric field. In a typical device, a liquid crystal layer (typically 10 μm thick) sits between two polarizers that are crossed (oriented at 90° to one another). The liquid crystal alignment is chosen so that its relaxed phase is a twisted one (see Twisted nematic field effect).[15] This twisted phase reorients light that has passed through the first polarizer, allowing its transmission through the second polarizer (and reflected back to the observer if a reflector is provided). The device thus appears transparent. When an electric field is applied to the LC layer, the long molecular axes tend to align parallel to the electric field thus gradually untwisting in the center of the liquid crystal layer. In this state, the LC molecules do not reorient light, so the light polarized at the first polarizer is absorbed at the second polarizer, and the device loses transparency with increasing voltage. In this way, the electric field can be used to make a pixel switch between transparent or opaque on command. Color LCD systems use the same technique, with color filters used to generate red, green, and blue pixels.[15] Similar principles can be used to make other liquid crystal based optical devices.[39]

Thermotropic chiral LCs whose pitch varies strongly with temperature can be used as crude thermometers, since the color of the material will change as the pitch is changed. Liquid crystal color transitions are used on many aquarium and pool thermometers as well as on thermometers for infants or baths.[40] Other liquid crystal materials change color when stretched or stressed. Thus, liquid crystal sheets are often used in industry to look for hot spots, map heat flow, measure stress distribution patterns, and so on. Liquid crystal in fluid form is used to detect electrically generated hot spots for failure analysis in the semiconductor industry.[41][42] Liquid crystal memory units with extensive capacity were used in Space Shuttle navigation equipment.[42]

Many common fluids, such as soap, are in fact liquid crystals. Soap forms a variety of LC phases depending on its concentration in water.[43]

See also

  • Biaxial nematic
  • Columnar phase
  • Chromonic
  • Liquid crystal display
  • Liquid crystal polymer
  • Lyotropic liquid crystal
  • Pattern formation
  • Plastic crystallinity
  • Smart glass
  • Thermochromics
  • Thermotropic crystal
  • Twisted nematic field effect
  • nematicon

References

  1. ↑ Liquid Crystals, S. Chandrasekhar, Cambridge University Press: 1994
  2. ↑ F. Reinitzer (1888). "Beiträge zur Kenntniss des Cholesterins". Monatshefte für Chemie (Wien) 9: 421–441. doi:10.1007/BF01516710. 
  3. ↑ O. Lehmann (1889). "Über fliessende Krystalle". Zeitschrift für Physikalische Chemie 4: 462–72. 
  4. ↑ T. J. Sluckin, D. A. Dunmur and H. Stegemeyer (2004). Crystals that Flow. Taylor and Francis. ISBN 0-415-25789-1. http://www.personal.soton.ac.uk/tim/crystals_that_flow/homepage.htm. 
  5. ↑ H. Kelker, B. Scheurle (1969). "A Liquid-crystalline (Nematic) Phase with a Particularly Low Solidification Point". Angew. Chem. Int. Ed. 8: 884. doi:10.1002/anie.196908841. 
  6. ↑ G. W. Gray, K. J. Harrison, J. A. Nash (1973). "New family of nematic liquid crystals for displays". Electronics Lett. 9: 130. doi:10.1049/el:19730096. 
  7. ↑ "History and Properties of Liquid Crystals". Nobelprize.org. http://nobelprize.org/educational_games/physics/liquid_crystals/history/. Retrieved 2009-06-06. 
  8. ↑ 8.0 8.1 8.2 8.3 8.4 8.5 de Gennes, P.G. and Prost, J (1993). The Physics of Liquid Crystals. Oxford: Clarendon Press. ISBN 0-19-852024-7. 
  9. ↑ 9.0 9.1 9.2 9.3 Chandrasekhar, S. (1992). Liquid Crystals (2nd ed.). Cambridge: Cambridge University Press. ISBN 0-521-41747-3. http://books.google.com/?id=TxvUxFlQsEsC&printsec=frontcover. 
  10. ↑ 10.0 10.1 10.2 I. Dierking (2003). Textures of Liquid Crystals. Weinheim: Wiley-VCH. ISBN 3-527-30725-7. http://books.google.com/?id=p-0xdzDRB2kC&printsec=frontcover. 
  11. ↑ 11.0 11.1 11.2 11.3 Collings, P.J. and Hird, M (1997). Introduction to Liquid Crystals. Bristol, PA: Taylor & Francis. ISBN 0-7484-0643-3. 
  12. ↑ Shao, Y.; Zerda, T. W. (1998). "Phase Transitions of Liquid Crystal PAA in Confined Geometries". Journal of Physical Chemistry B 102 (18): 3387–3394. doi:10.1021/jp9734437. 
  13. ↑ Rego, J.A.; Harvey, Jamie A.A.; MacKinnon, Andrew L.; Gatdula, Elysse (January 2010). "Asymmetric synthesis of a highly soluble ‘trimeric’ analogue of the chiral nematic liquid crystal twist agent Merck S1011". Liquid Crystals 37 (1): 37–43. doi:10.1080/02678290903359291. http://www.csupomona.edu/~jarego/pubs/RD2_LC.pdf. 
  14. ↑ L. A. Madsen, T. J. Dingemans, M. Nakata, and E. T. Samulski (2004). "Thermotropic Biaxial Nematic Liquid Crystals". Phys. Rev. Lett. 92: 145505. doi:10.1103/PhysRevLett.92.145505. 
  15. ↑ 15.0 15.1 15.2 Joseph A. Castellano (2005). Liquid Gold: The Story of Liquid Crystal Displays and the Creation of an Industry. World Scientific Publishing. ISBN 978-9812389565. 
  16. ↑ Kopp, V. I.; Fan, B.; Vithana, H. K. M.; Genack, A. Z. (1998). "Low threshold lasing at the edge of a photonic stop band in cholesteric liquid crystals". Opt. Lett 23 (21): 1707–1709. doi:10.1364/OL.23.001707. PMID 18091891. http://www.opticsinfobase.org/abstract.cfm?id=62754. 
  17. ↑ T. J. Sluckin, D. A. Dunmur and H. Stegemeyer (2004). Crystals That Flow – classic papers from the history of liquid crystals. London: Taylor & Francis. ISBN 0-415-25789-1. http://books.google.com/?id=iMEMAuxrhFcC&printsec=frontcover. 
  18. ↑ E. B. Priestley, P. J. Wojtowicz and P. Sheng (1974). Introduction to Liquid Crystals. Plenum Press. ISBN 0-306-30858-4. 
  19. ↑ Harry J. Coles, Mikhail N. Pivnenko (2005). "Liquid crystal 'blue phases' with a wide temperature range". Nature 436 (7053): 997–1000. doi:10.1038/nature03932. PMID 16107843. http://www.nature.com/nature/journal/v436/n7053/abs/nature03932.html. 
  20. ↑ Jun Yamamoto, Isa Nishiyama, Miyoshi Inoue and Hiroshi Yokoyama (2005). "Optical isotropy and iridescence in a smectic blue phase". Nature 437: 525. http://www.nature.com/nature/journal/v437/n7058/abs/nature04034.html. 
  21. ↑ Kikuchi H, Yokota M, Hisakado Y, Yang H, Kajiyama T. (2002). "Polymer-stabilized liquid crystal blue phases". Nature Materials 1 (1): 64. doi:10.1038/nmat712. PMID 12618852. http://www.nature.com/nmat/journal/v1/n1/full/nmat712.html. 
  22. ↑ "Samsung Develops World’s First 'Blue Phase' Technology to Achieve 240 Hz Driving Speed for High-Speed Video". http://www.physorg.com/news129997960.html. Retrieved 23 april 2009. 
  23. ↑ James D. Martin, Cristin L. Keary, Todd A. Thornton, Mark P. Novotnak, Jeremey W. Knutson and Jacob C. W. Folmer (2006). "Metallotropic liquid crystals formed by surfactant templating of molten metal halides". Nature Materials 5 (4): 271. doi:10.1038/nmat1610. PMID 16547520. 
  24. ↑ A. Buka et al. (1987). "Viscous fingering in liquid crystals". Phys. Rev. A 36: 3984. doi:10.1103/PhysRevA.36.3984. 
  25. ↑ R. Gonzalez-Cinca et al. (1996). "Phase-field simulations and experiments of faceted growth in liquid crystal". Physica D 99: 359. doi:10.1016/S0167-2789(96)00162-5. 
  26. ↑ R. González-Cinca et al. (1998). "Heat diffusion anisotropy in dendritic growth: phase field simulations and experiments in liquid crystals". Journal of Crystal Growth 193: 712. doi:10.1016/S0022-0248(98)00505-3. 
  27. ↑ S. K. Ghosh (1984). "A model for the orientational order in liquid crystals". Il Nuovo Cimento D 4: 229. doi:10.1007/BF02453342. 
  28. ↑ L. Onsager (1949). "The effects of shape on the interaction of colloidal particles". Ann. N.Y. Acad. Sci. 51: 627. doi:10.1111/j.1749-6632.1949.tb27296.x. 
  29. ↑ 29.0 29.1 G.J. Vroege and H.N.W. Lekkerkerker (1992). "Phase transitions in lyotropic colloidal and polymer liquid crystals". Rep. Progr. Phys. 55: 1241. doi:10.1088/0034-4885/55/8/003. 
  30. ↑ W. Maier and A. Saupe (1958). "Eine einfache molekulare theorie des nematischen kristallinflussigen zustandes" (in German). Z. Naturforsch. A 13: 564. 
  31. ↑ W. Maier and A. Saupe (1959). "Eine einfache molekular-statistische theorie der nematischen kristallinflussigen phase .1" (in German). Z. Naturforsch. A 14: 882. 
  32. ↑ W. Maier and A. Saupe (1960). "Eine einfache molekular-statistische theorie der nematischen kristallinflussigen phase .2" (in German). Z. Naturforsch. A 15: 287. 
  33. ↑ W.L. McMillan (1971). "Simple Molecular Model for the Smectic A Phase of Liquid Crystals". Phys. Rev. A 4: 1238. doi:10.1103/PhysRevA.4.1238. 
  34. ↑ F. M. Leslie (1992). "Continuum theory for nematic liquid crystals". Continuum Mechanics and Thermodynamics 4: 167. doi:10.1007/BF01130288. http://www.springerlink.com/content/u5w745n0v7318621/. 
  35. ↑ H. Fujikake et al. (1998). "Video camera system using liquid-crystal polarizing filter toreduce reflected light". IEEE Transactions on Broadcasting 44: 419. doi:10.1109/11.735903. 
  36. ↑ M.F. Achard et al. (2003). "Switching of banana liquid crystal mesophases under field". The European Physical Journal E 10 (2): 129. doi:10.1140/epje/e2003-00016-y. PMID 15011066. 
  37. ↑ Marc Baus and Jean-Louis Colot (1989). "Ferroelectric nematic liquid-crystal phases of dipolar hard ellipsoids". Phys. Rev. A 40: 5444. doi:10.1103/PhysRevA.40.5444. http://link.aps.org/doi/10.1103/PhysRevA.40.5444. 
  38. ↑ H. Uehara and J. Hatano (2002). "Pressure-Temperature Phase Diagrams of Ferroelectric Liquid Crystals". J. Phys. Soc. Jpn. 71: 509. doi:10.1143/JPSJ.71.509. http://jpsj.ipap.jp/link?JPSJ/71/509/. 
  39. ↑ T. T. Alkeskjold et al. (2007). "Integrating liquid crystal based optical devices in photonic crystal". Optical and Quantum Electronics 39: 1009. doi:10.1007/s11082-007-9139-8. 
  40. ↑ Pool thermometer – US Patent 4738549
  41. ↑ "Hot-spot detection techniques for ICs". http://www.acceleratedanalysis.com/LC_hotspotdetection_procedure.html. Retrieved 2009-05-05. 
  42. ↑ 42.0 42.1 Alexander Bolonkin (2007). "Control of Regional and Global Weather". arΧiv:physics/0701097v1 [physics.gen-ph]. http://arxiv.org/ftp/physics/papers/0701/0701097.pdf. 
  43. ↑ V. Luzzati et al. (1957). "Structure of the Liquid-Crystal Phases of the Soap–water System: Middle Soap and Neat Soap". Nature 180: 600. doi:10.1038/180600a0. http://www.nature.com/nature/journal/v180/n4586/abs/180600a0.html. 

External links

States of matter
Phase change - en.svg
Low energy
Bose–Einstein condensate · Fermionic condensate · Quantum Hall · Rydberg matter · Strange matter · Superfluid · Supersolid
High energy
Degenerate matter · QCD matter · Quark–gluon plasma  · Supercritical fluid
Other states
Colloid · Glass · Liquid crystal · Magnetically ordered (Antiferromagnet, Ferrimagnet, Ferromagnet) · String-net liquid · Superglass
Transitions
Boiling · Boiling point · Critical line · Critical point · Crystallization · Deposition · Evaporation · Flash evaporation · Freezing · Lambda point · Melting · Melting point · Regelation · Saturated fluid · Sublimation · Supercooling · Triple point
Quantities
Enthalpy of fusion · Enthalpy of sublimation · Enthalpy of vaporization · Latent heat · Latent internal energy · Trouton's constant · Trouton's ratio · Volatility
Concepts
Binodal · Compressed fluid · Cooling curve · Equation of state · Leidenfrost effect · Mpemba effect · Order and disorder (physics) · Spinodal · Superconductivity · Superheated vapor · Superheating · Thermo-dielectric effect